고등학교 이후로 진짜 오랜만에 듣는 평균, 분산, 표준편차 어쩌구들..
분명 이과가 아니었던 적이 없는데,, 기본 개념들을 다시 마주하니 익숙한듯 익숙하지 않다ㅜ_ㅜ
1. 분산과 표준편차 (분산 = (표준편차)**2)
- 값들이 평균으로부터 얼마나 벗어나 있는지 (이탈도, deviation)를 나타내는 값
- 평균 : .mean() / 분산 : .var() / 표준편차 : .std()
a = np.array([180,173,165,166,171])
print(f'평균 : {a.mean()}')
print(f'분산 : {a.var()}')
print(f'표준편차 : {a.std()}')
2. 평균 비교
(1) 표준오차 (SE, standard error)
- 표준오차는 표준편차와 아예! 다른 개념 (표준편차와 비교X)
- 표본의 평균과 모집단의 평균과의 오차!!
(2) 95% 신뢰구간
① 임의의 모집단 준비
- 원래는 모집단을 알 수 없음! 전지적 분석가 시점에서 살펴보는 것임.
# 임의의 모집단 생성
pop = [round(rd.normalvariate(172, 7),1) for i in range(800000)]
# 시각화
plt.figure(figsize=(10,6))
sns.histplot(pop, bins = 100)
plt.axvline(np.mean(pop), color = 'r')
plt.text(np.mean(pop)+1, 30000, f'pop mean : {np.mean(pop).round(3)}', color = 'r')
plt.show()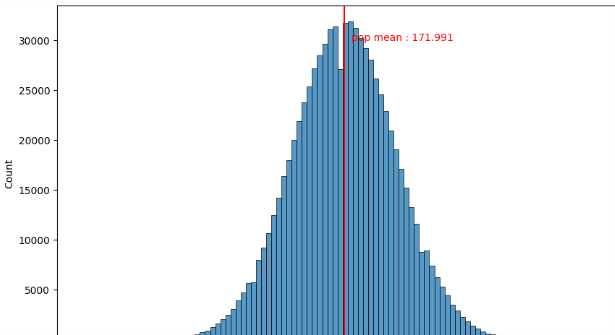
② 표본 조사 (50명을 임의로 샘플링)
x_mean = []
# rd => import random as rd : 랜덤으로 처리
# 아래 표본조사(50씩) 100번 실행
# 랜덤으로 처리하기 때문에 돌릴 때마다 달라짐
for i in range(100):
s1 = rd.sample(pop, 50)
s1 = pd.Series(s1)
x_mean.append(round(s1.mean(),3))리
x_mean (표본조사 랜덤한 50개의 평균이 100개 들어있음)
plt.figure(figsize=(10,6))
sns.kdeplot(x_mean)
plt.axvline(np.mean(x_mean), color = 'r')
plt.text(np.mean(x_mean)+1, 0.1, f'pop mean : {round(np.mean(x_mean),3)}', color = 'r')
plt.show()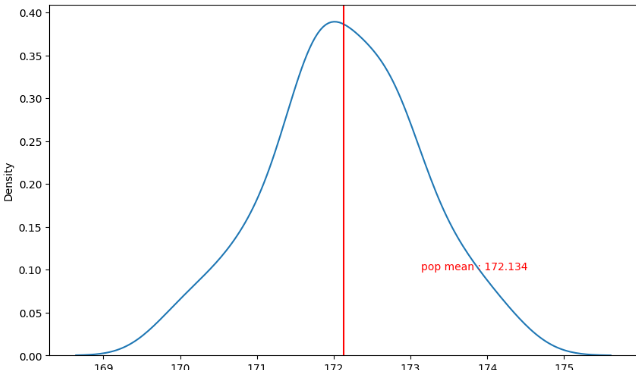
③ 95% 신뢰구간
s1.mean() - (1.96 * s1.sem()), s1.mean() + (1.96 * s1.sem())
# 결과
(170.3997394714916, 173.85626052850836)
④ 95% 신뢰구간에 대한 실험
- 샘플조사 100번 수행하였을때, 그때마다 신뢰구간을 계산한 후
- 그 중 몇번이 모평균ㅇ르 포함하는지 확인
- 95% 신뢰구간일 경우, 100번 중 95번은 모평균을 포함함.
# 100번 샘플링
samples = { 'id' : [], 'value' : []}
for i in range(100) :
samples['id'] += [i]* 100
samples['value'] += rd.sample(pop,100)
samples = pd.DataFrame(samples)
samples.shape # (10000, 2) 10,000개의 행과 2개의 열# errorbar 라는 차트
# 신뢰구간, 표준오차 구간을 시각화 하는 방법
plt.figure(figsize = (18, 8))
sns.pointplot(x = 'id', y = 'value', data = samples, join = False)
plt.axhline(np.mean(pop), color = 'r')
plt.show()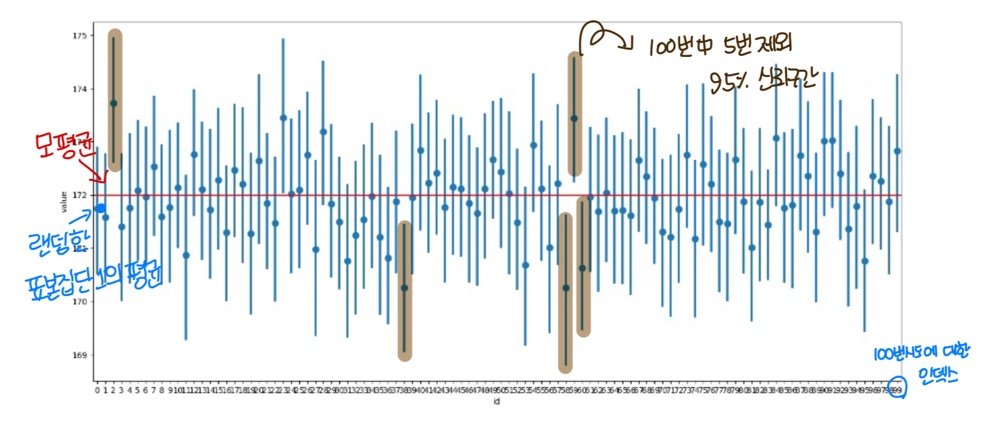
100개의 표본집단의 평균의 평균과 모평균의 차이가 표준오차이고, 그로부터 신뢰구간 95% 계산한다.
3. 중심극한 정리
- 표본이 클수록, 표집분포는 정규분포에 가까워짐.
① 정규분포 실험
# 임의의 모집단 만들기
pop = [round(rd.expovariate(.3)+165,2) for i in range(10001)]
# 표본의 크기
n = 100
# 표본의 갯수
m = 200
sample_mean = [np.mean(rd.sample(pop,n)) for i in range(m)]
plt.figure(figsize=(10,6))
sns.kdeplot(sample_mean)
plt.axvline(x=np.mean(sample_mean), color = 'red') #표본평균들의 평균
plt.axvline(x=np.mean(pop), color = 'grey') # 모평균
plt.text(np.mean(sample_mean)-.2, 0.02, round(np.mean(sample_mean),3), color = 'red') #표본평균들의 평균
plt.text(np.mean(pop)+.1,0.02, round(np.mean(pop),3), color = 'grey') #모평균
plt.show() # show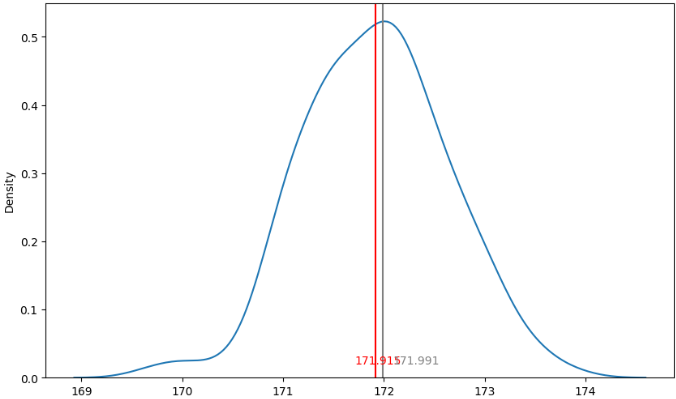
② 표본의 크기에 따른 정규분포
- 표본의 크기가 클수록 정규분포의 모양에 가까워지며 밀도가 높아진다.
'파이썬 > 데이터 분석' 카테고리의 다른 글
| [240930] 데이터 분석 #6 이변량 - 범주 vs 범주 (0) | 2024.10.01 |
|---|---|
| [240927] 데이터 분석 #5 이변량 - 범주 vs 숫자 (0) | 2024.09.27 |
| [240926] 데이터 분석 #3 이변량 - 숫자 vs 숫자 (0) | 2024.09.27 |
| [240926] 데이터 분석 #2 개별 변수 분석 - 범주형 변수 (2) | 2024.09.27 |
| [240925] 데이터 분석 #1 개별 변수 분석 - 숫자형 변수 (1) | 2024.09.25 |



